本节主要介绍了线性分组码、循环码、卷积码的编码与译码。
信道编码的基本概念
信道编码的目的:提高信号传输的可靠性
信道编码的方法:增加冗余比特,以发现或纠正错误
信道编码的实质:在信息码中增加一定数量的多余码元(称为监督码元),是它们满足一定的约束关系
- 发送端将信息码元和监督码元共同组成一个由信道传输的码字
- 一旦传输过程中发生错误,则信息码元和监督码元间的约束关系被破坏
- 在接收端按既定的规则校验这种约束关系,从而可达到发现和纠正错误的目的
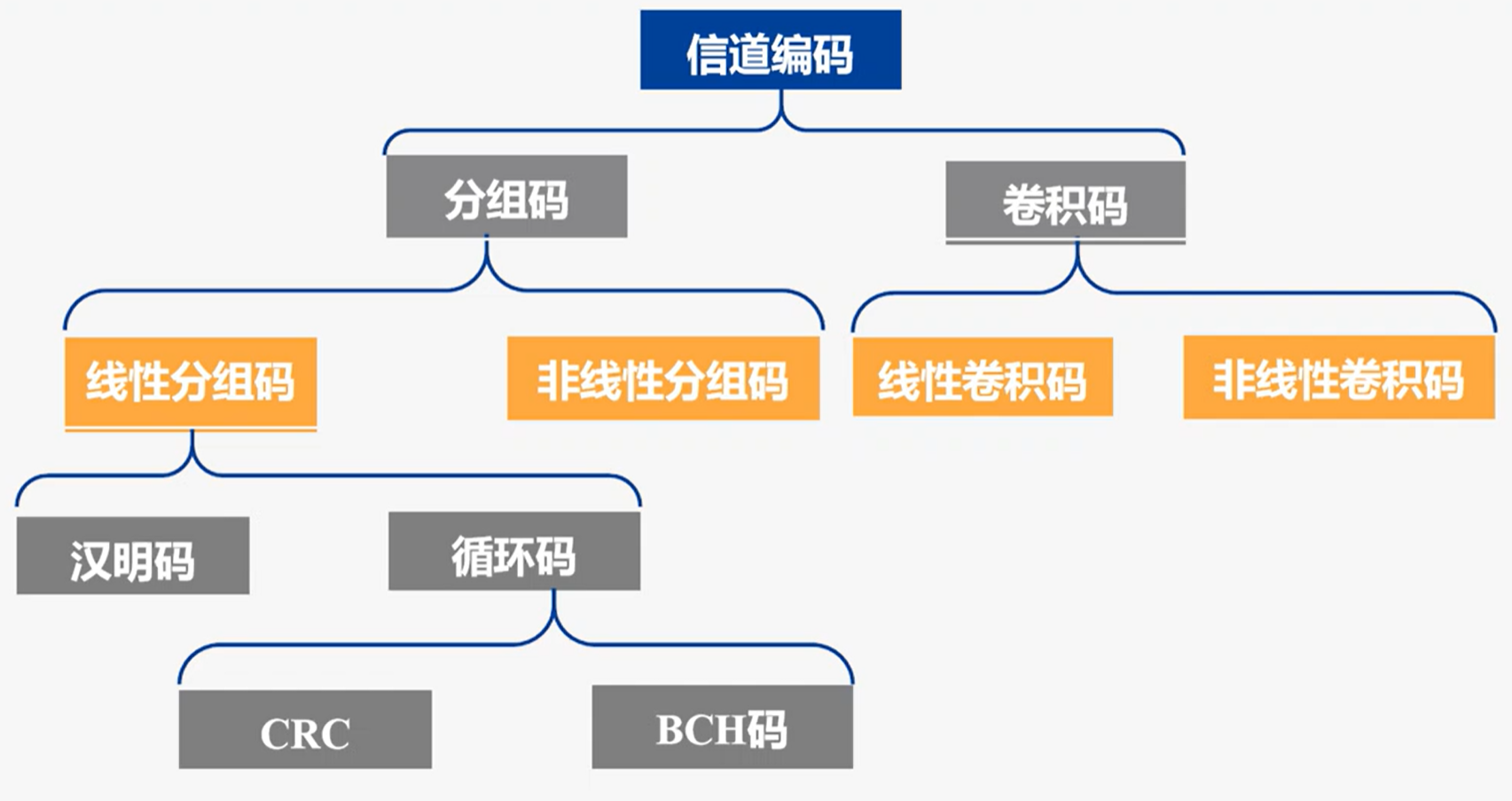
信道编码的分类:
- 线性与非线性码:
- 线性码:信息码与监督码之间的关系为线性关系
- 非线性码:信息码与监督码之间的关系为非线性关系
- 分组码与卷积码:
- 分组码:信息码与监督码以组为单位建立关系
- 卷积码:监督码与本组和前面码组中的信息码有关
- 系统码与非系统码:
- 系统码:编码后码组中信息码保持原图样顺序不变
- 非系统码:编码后码组中原信息码原图样发生变化
- 线性与非线性码:
误码的主要形式:
- 随机错误:误码的位置随机(误码间无关联),随机误码主要由白噪声引起
- 突发错误:误码成串出现,主要由强脉冲及雷电等突发的强干扰引起的
- 混合错误:以上两种误码及产生原因的组合
编码效率与冗余度:
- 假设分组码的长度为n,其中信息位为k,相应的监督位为n-k
- 编码效率越高,意味着冗余度越低
基本术语:
- 码重W:码组/码字中非零码元的数目
- 码距d(Hamming距):两码组/码字中对应码元位置上取值不同的个数称为码组/码字间的距离,简称码距
- 最小码距$d_{min}$:准用码组/码字空间中任意两码组间的最小距离
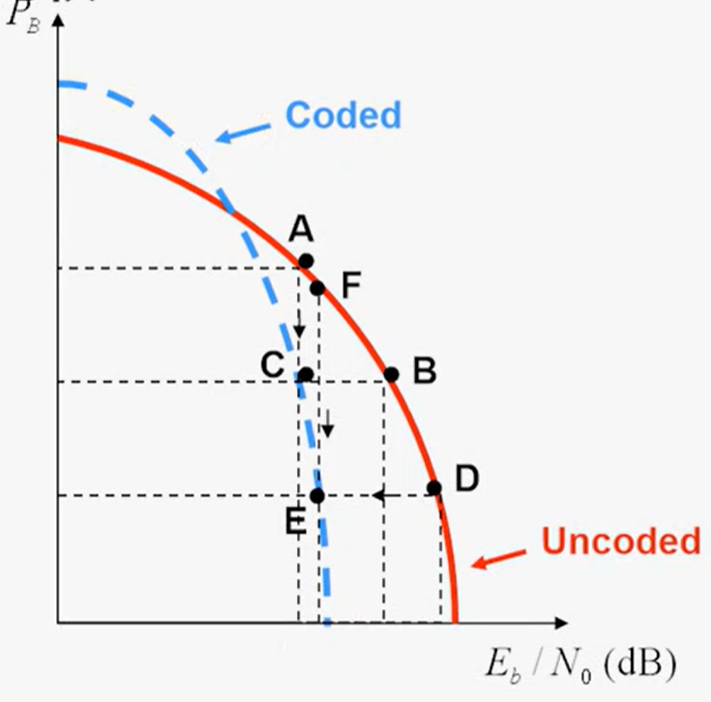
一般情况下,编码后,在同样的$\frac {E_b}{N_0}$下,编码后系统有更好的性能
线性分组码
定义:
- 把信源输出的k位信息序列,通过编码器产生r个监督位,输出长为n=k+r的码字,所得码字的全体,称为(n,k)线性分组码
- 码组中的信息位与监督位之间的关系由线性方程确定
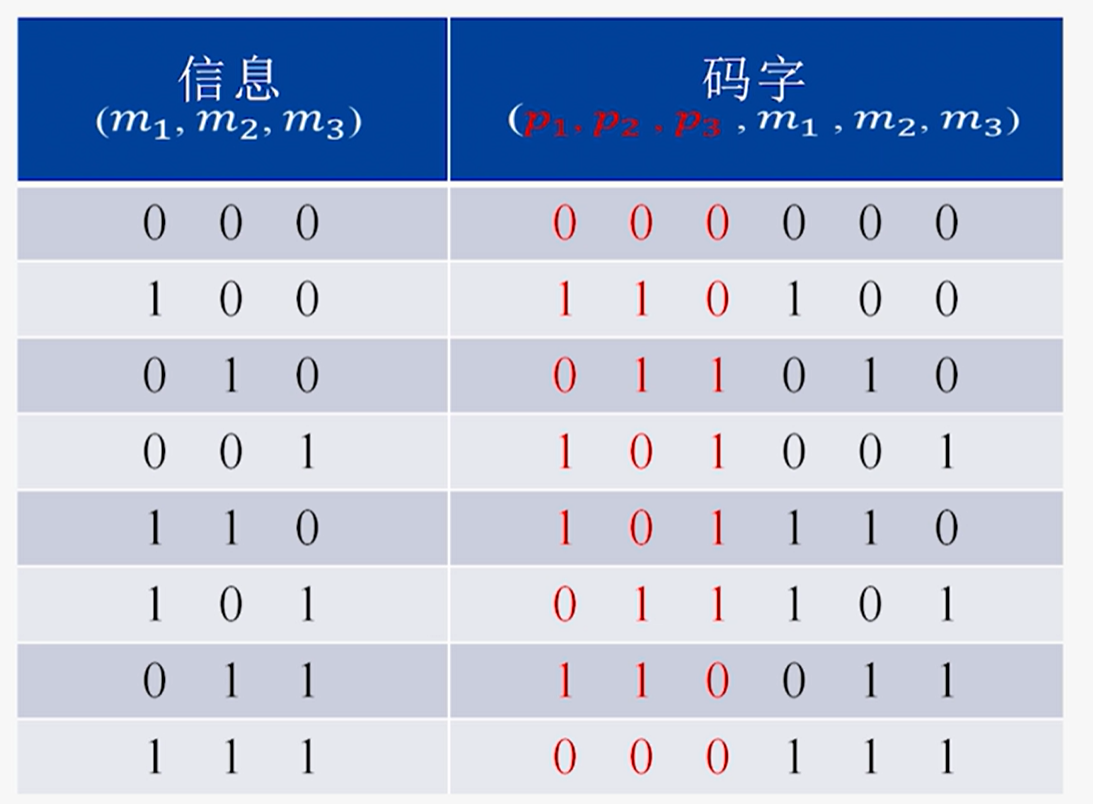
生成矩阵:从(n,k)线性分组码中任取k个线性无关的码字,按行的形式写出矩阵G,则称该线性分组码为生成矩阵
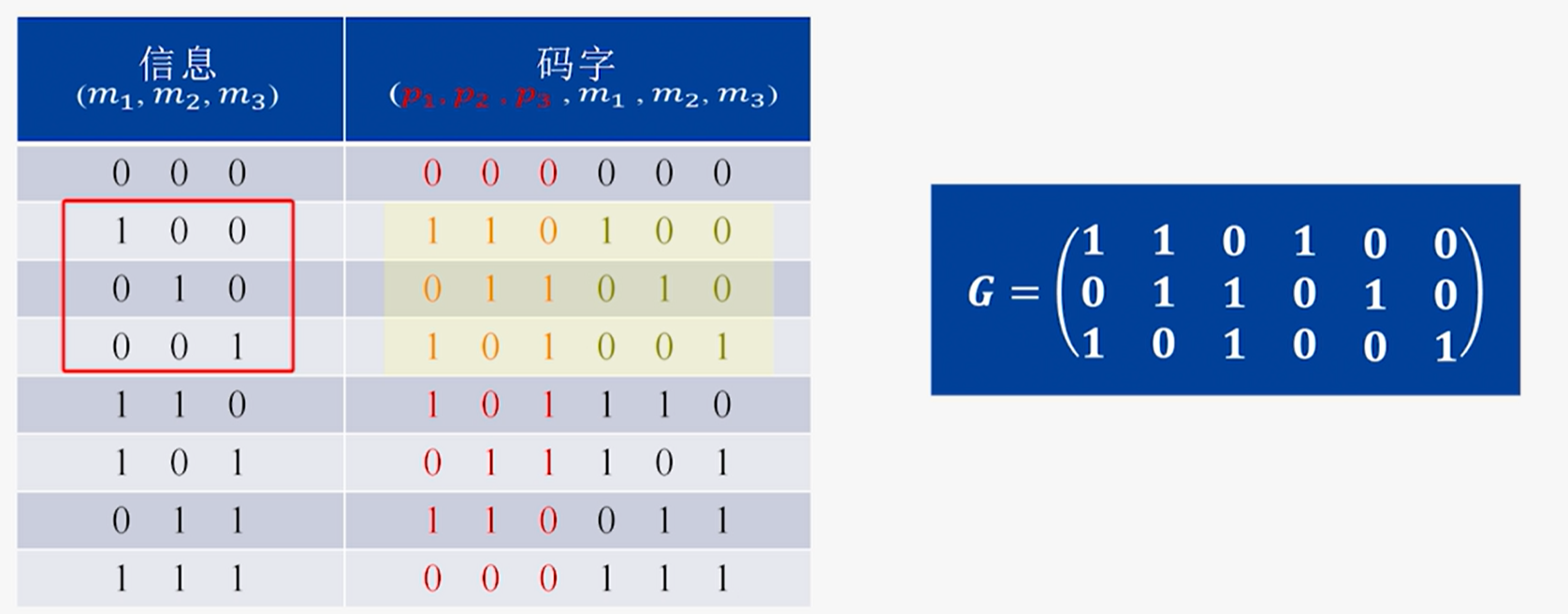
通过$U=mG$(m为输入信息)便能计算出编码后的码字$U$
监督矩阵:
在无误码存在的条件下,存在如下约束关系:
伴随式:
$(n,k)$线性分组码的译码方法:
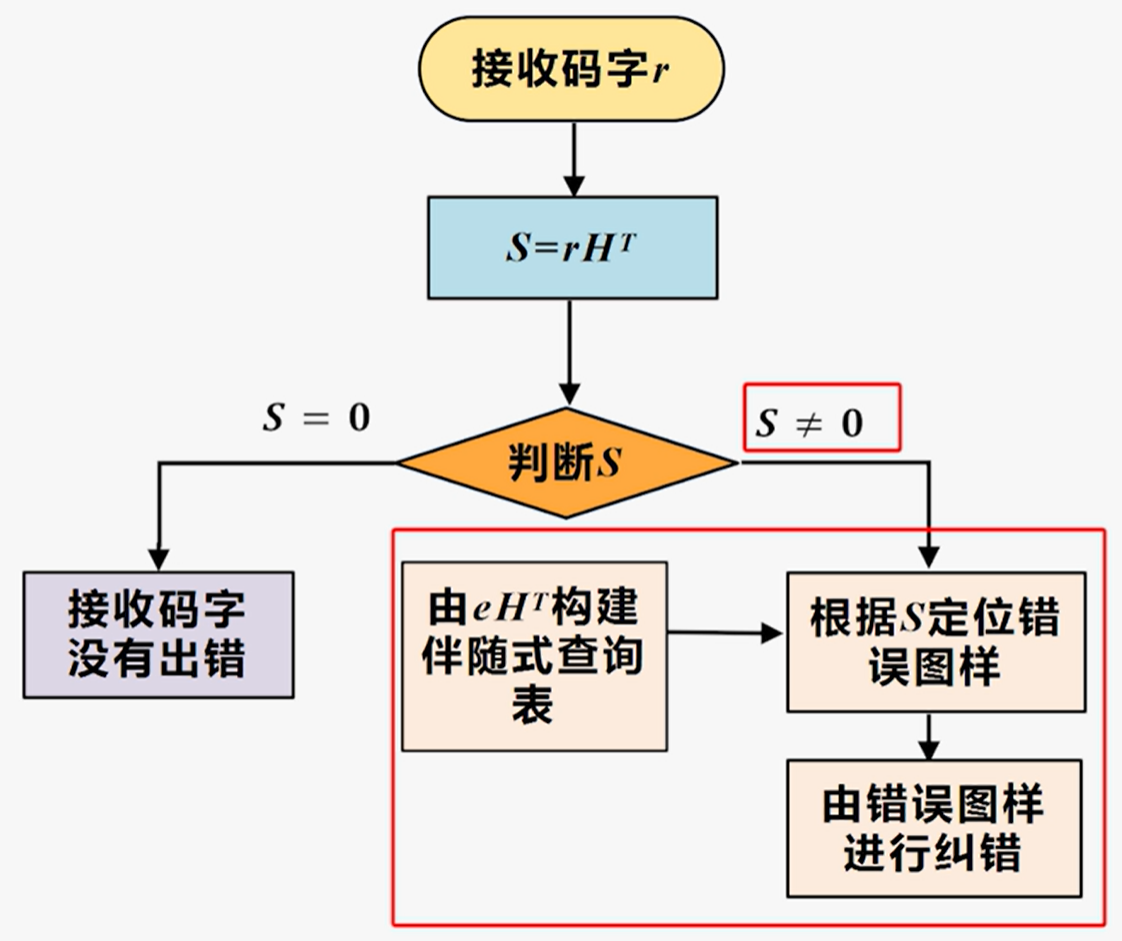
由$eH^T(e为错误图样)$构建伴随式错误图样查询表
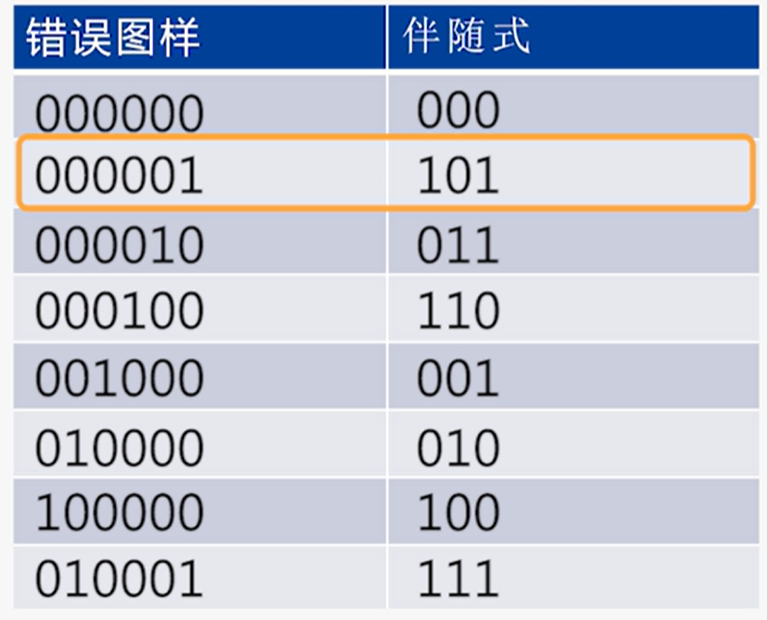
例:

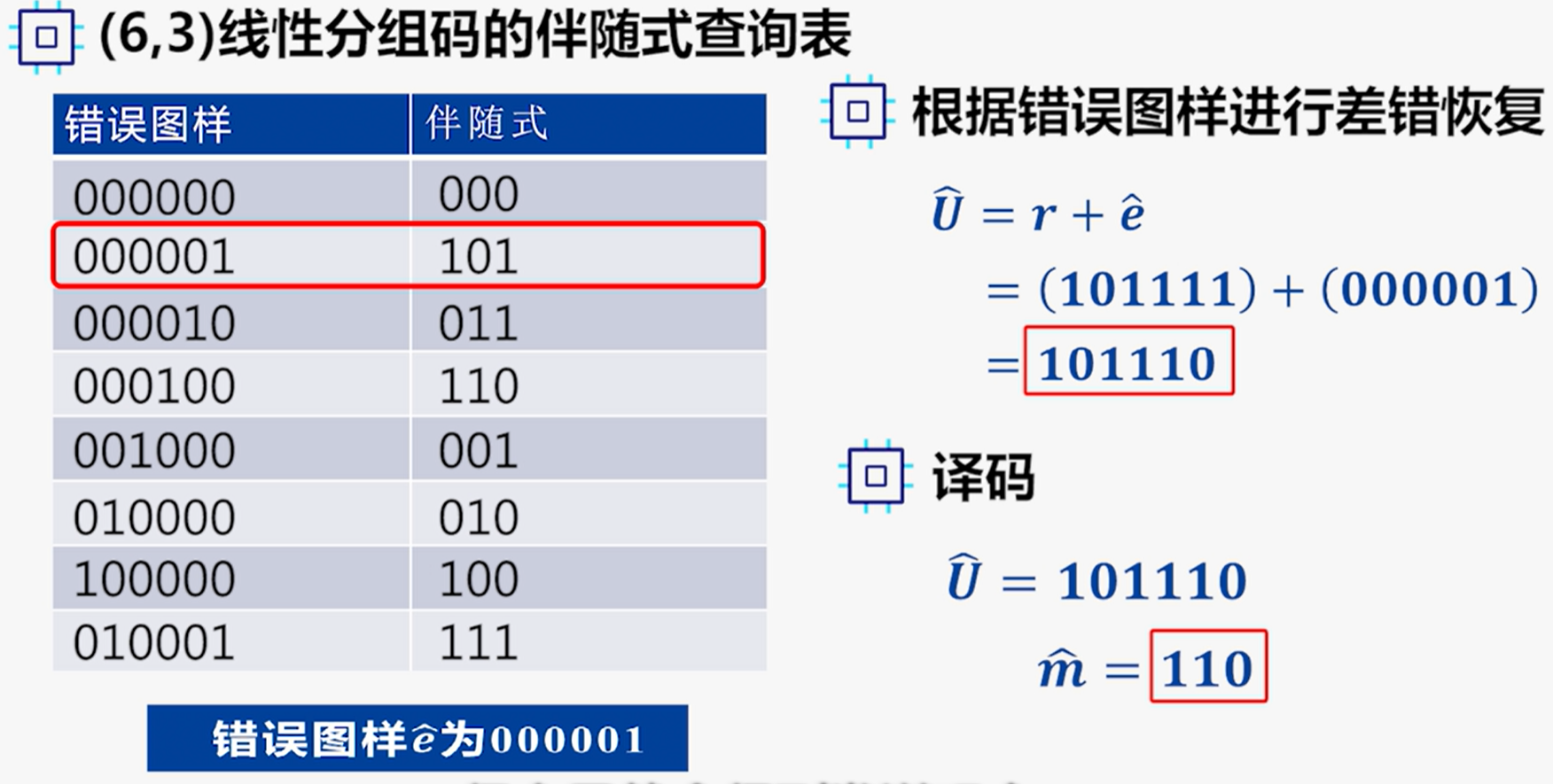
线性分组码的检错与纠错能力:任意一个$(n,k)$分组码,若要在任何码字内:
- 能检测e个随机错误,则要求最小Hamming距离$d\ge e+1$
- 能纠正t个随机错误,则要求$d\ge 2t+1$
- 能纠正t个随机错误,同时检测出$e(\ge t)$个错误,则要求$d\ge t+e+1$
循环码
定义:码长为n,信息位为k的$(n,k)$线性分组码,若具有下列属性:
生成多项式$g(x)$与码字多项式$U(x)$存在约束关系:
例:
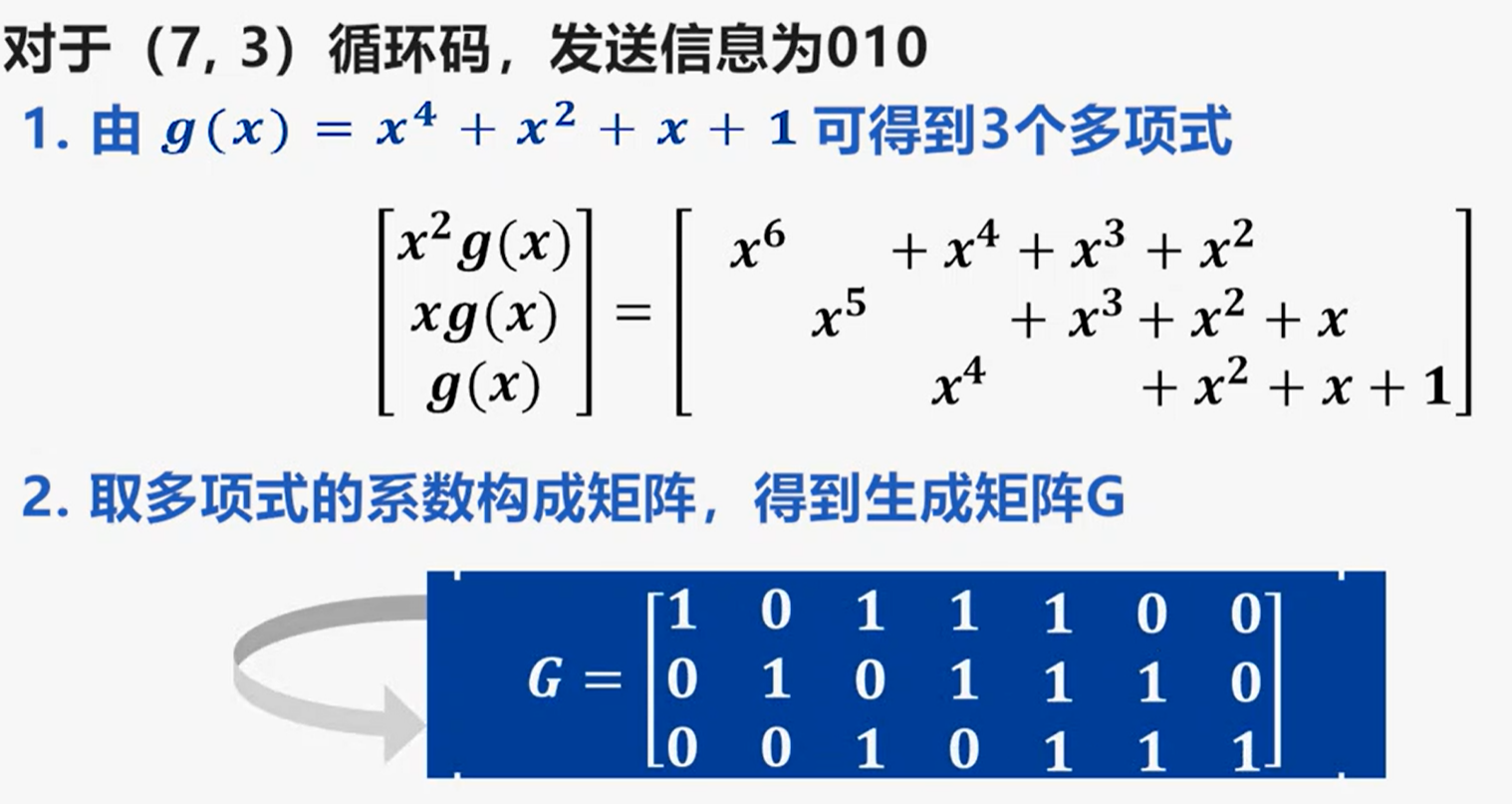

伴随式:伴随式可以由$r(x)$对生成多项式$g(x)$取模计算得到:
译码方法:
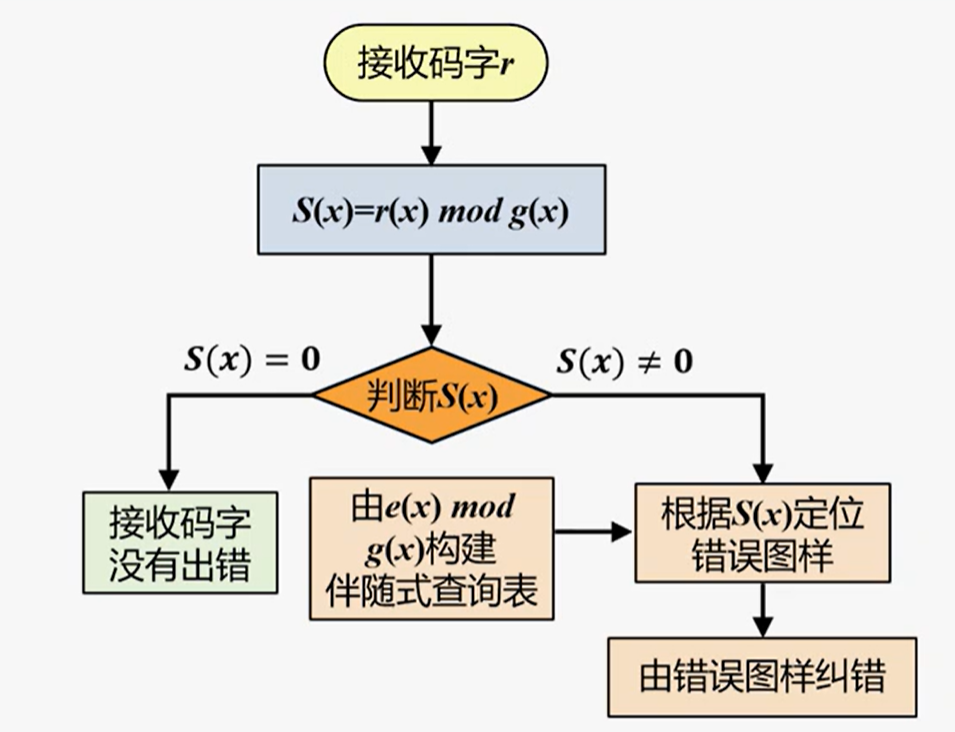
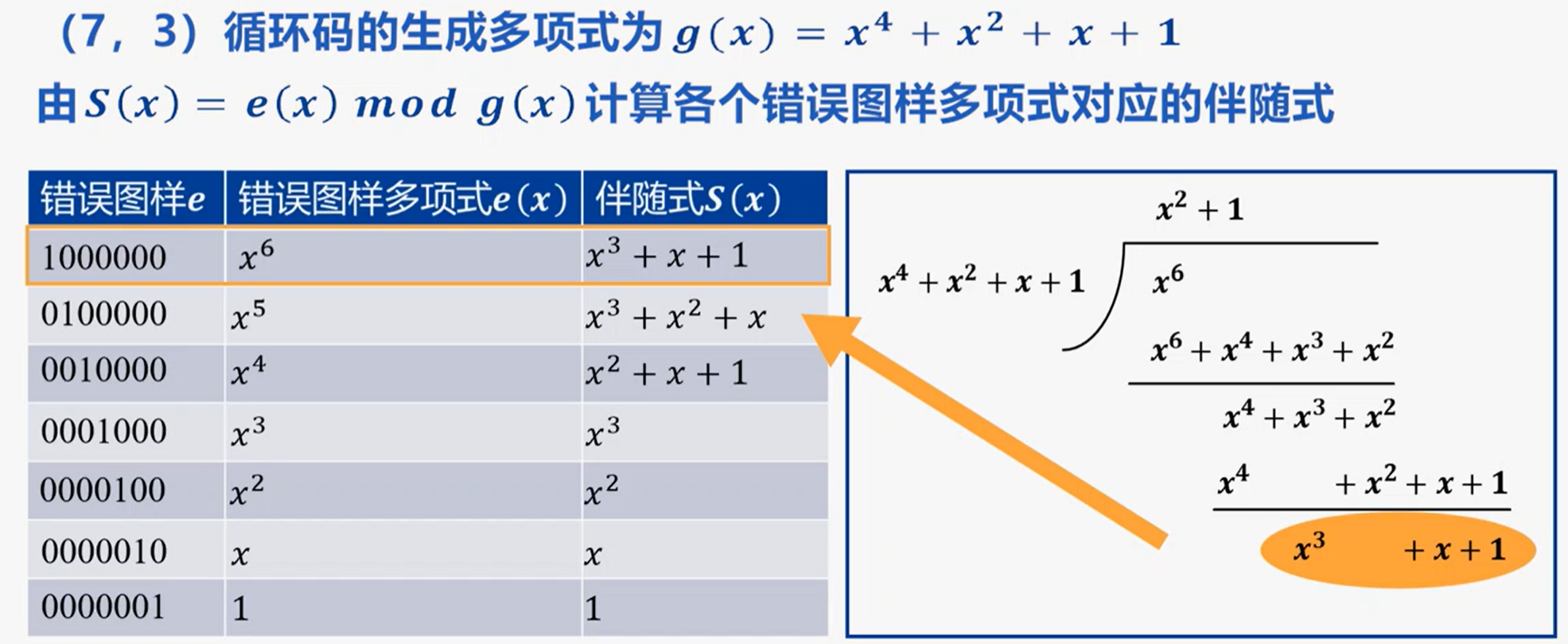
构建伴随式查询表:
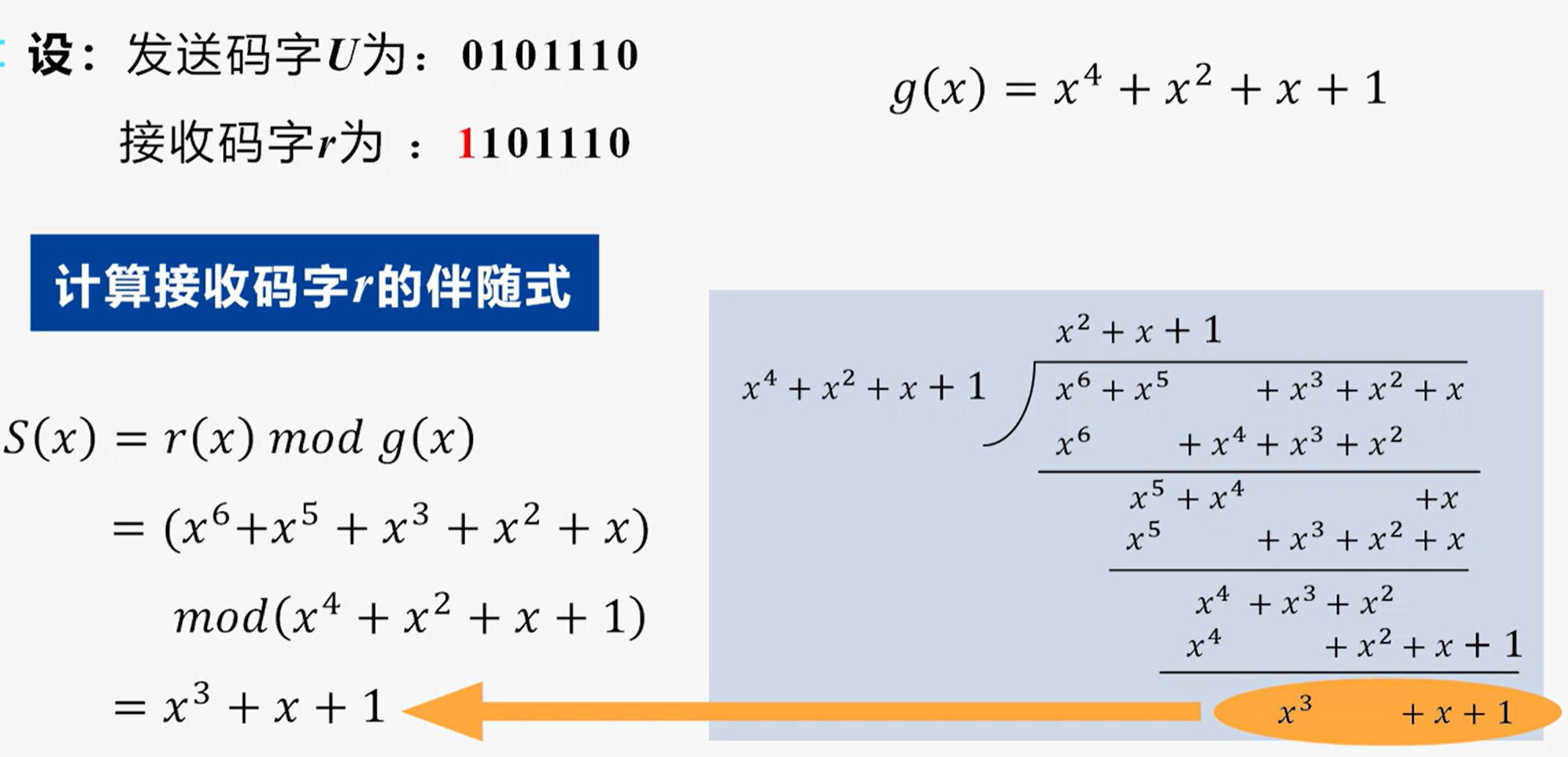
例:
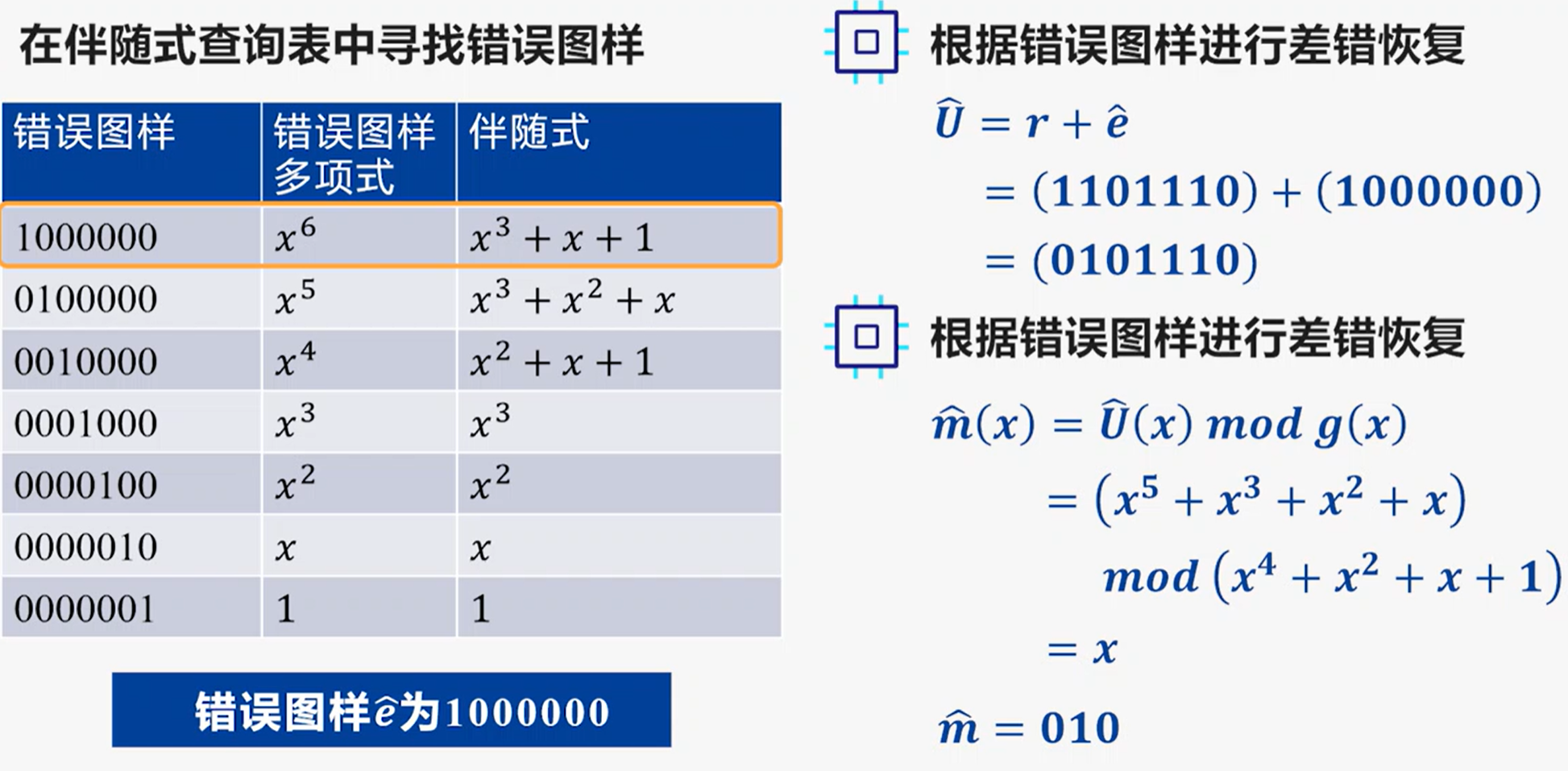
卷积码的基本概念
卷积码:通过将输入信息序列与编码器做卷积运算,将k位信息编成n比特,此n比特不仅与当前k位信息有关,还与前面(m-1)段的信息有关
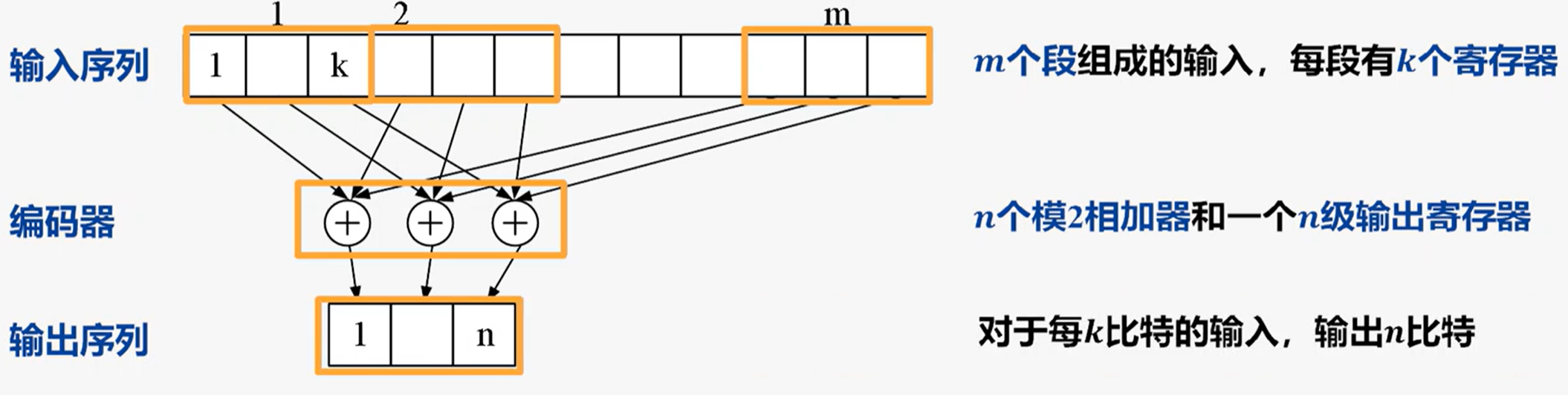
卷积码$(n,k,m)$的参数:
- $k$:输入比特信息
- $n$:输出码字
- $m$:约束长度,即移位寄存器的级数
- $R$:码率,表示传输信息的有效性$R=\frac kn$
1.卷积码的编码方法—冲击响应
假设为卷积码$(2,1,3)$,即输入1bit,输出2bit,移位寄存器的个数为3
输入”1”时对应的输出序列为:
11 10 11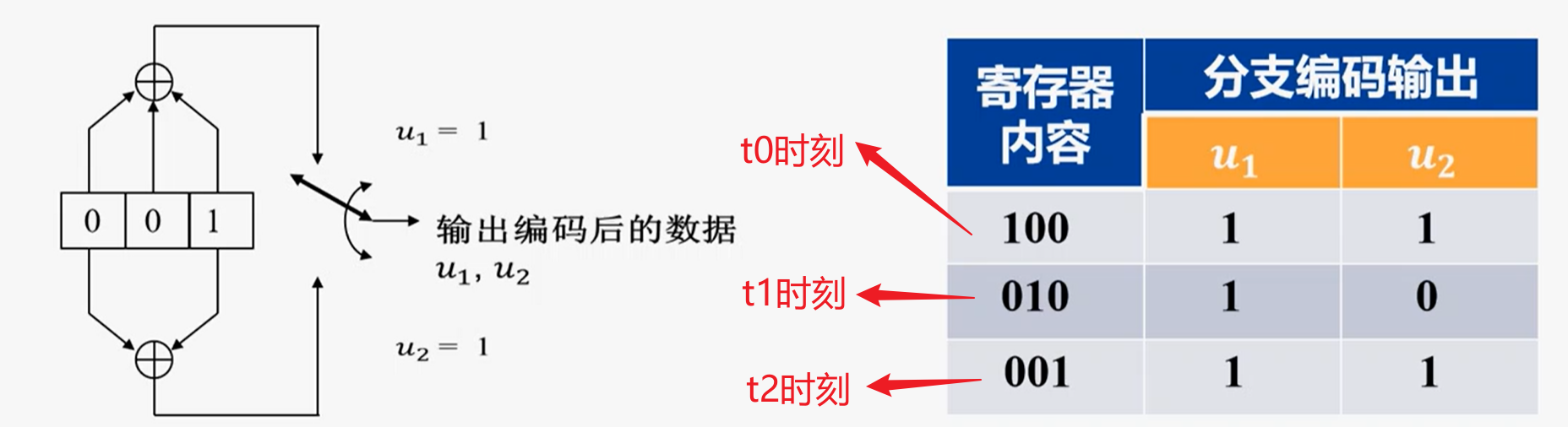
则当输入序列为m=101时对应的输出可按照输入的线性叠加方式得到:
11 10 00 10 11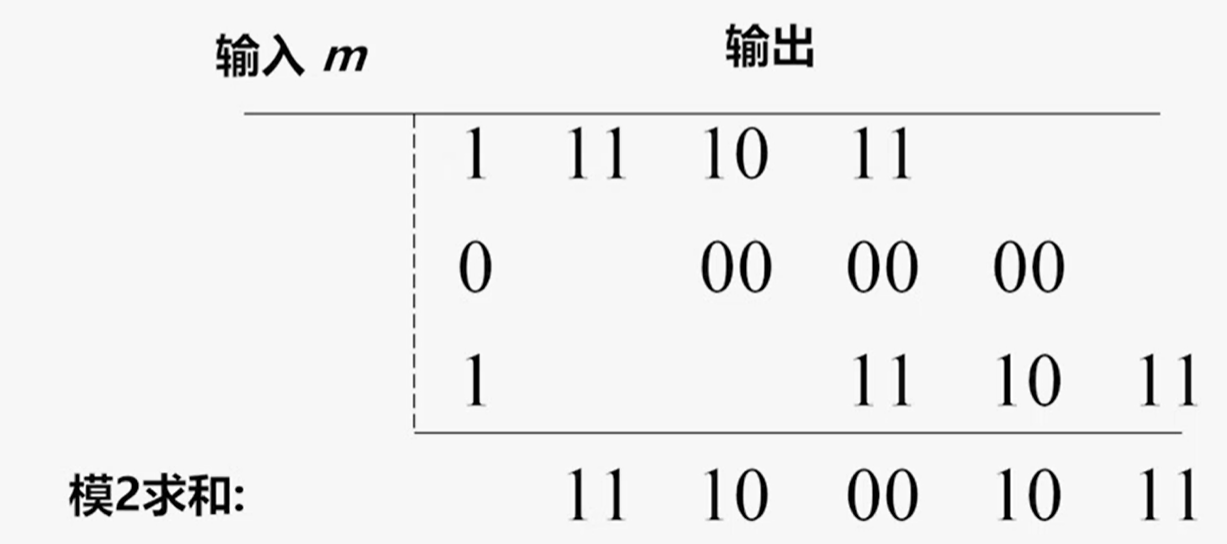
2.卷积码的编码方法—状态描述和状态图
可以用当前输入和之前(m-1)个输入来预测输出
卷积编码器中,状态共有$2^{m-1}$个
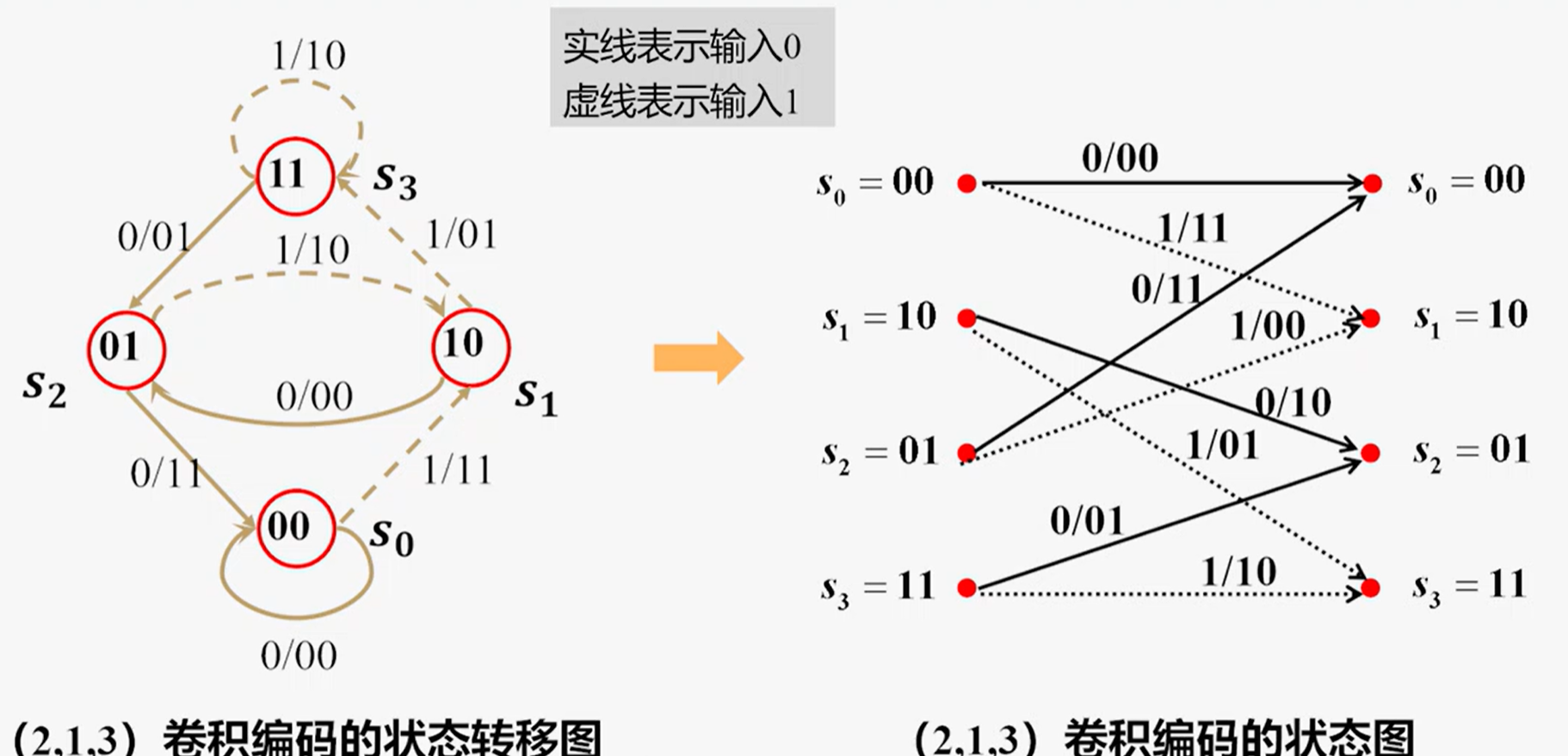
$(2,1,3)$卷积码的编码方法
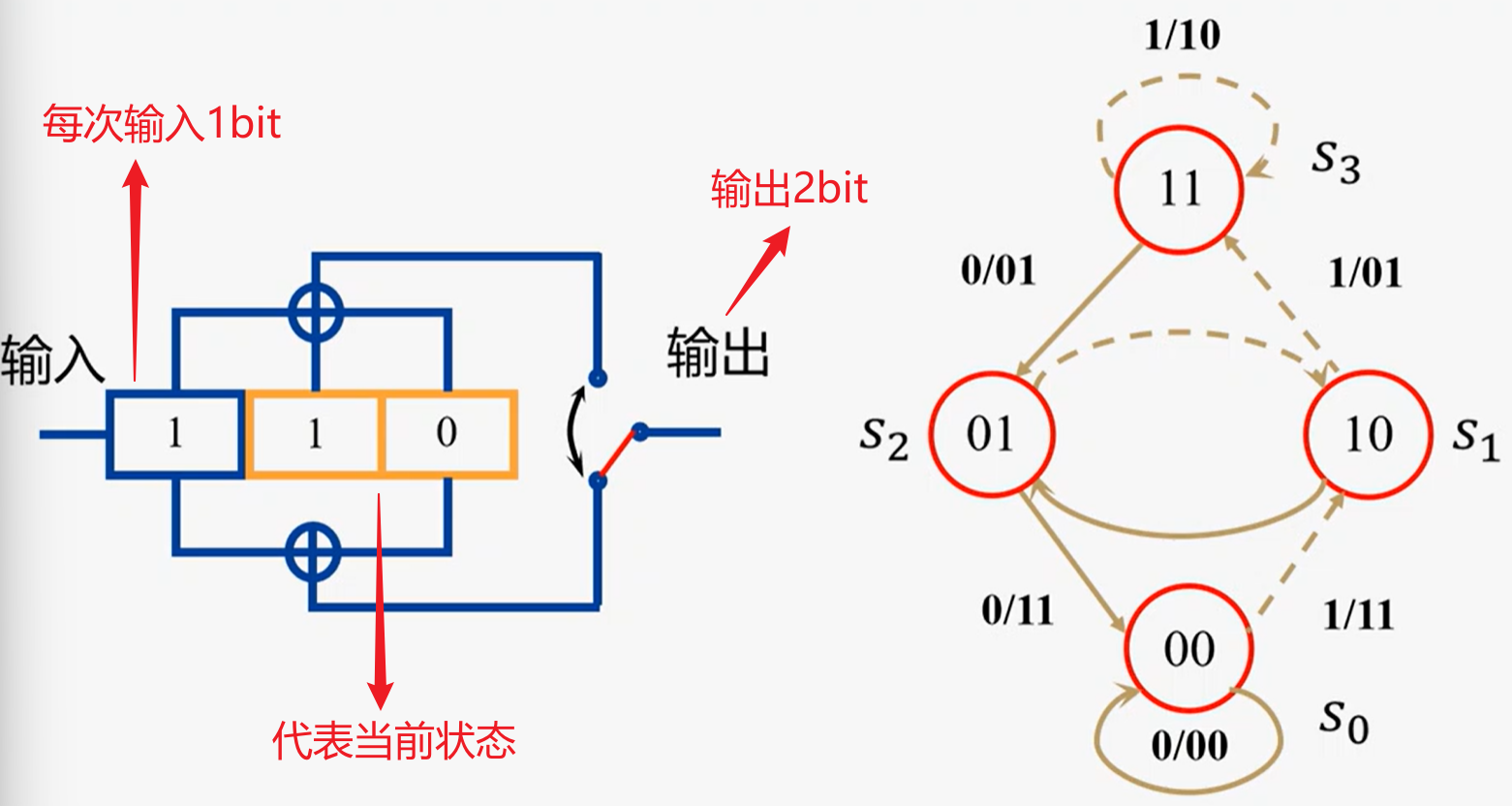
$(2,1,3)$卷积编码的状态图
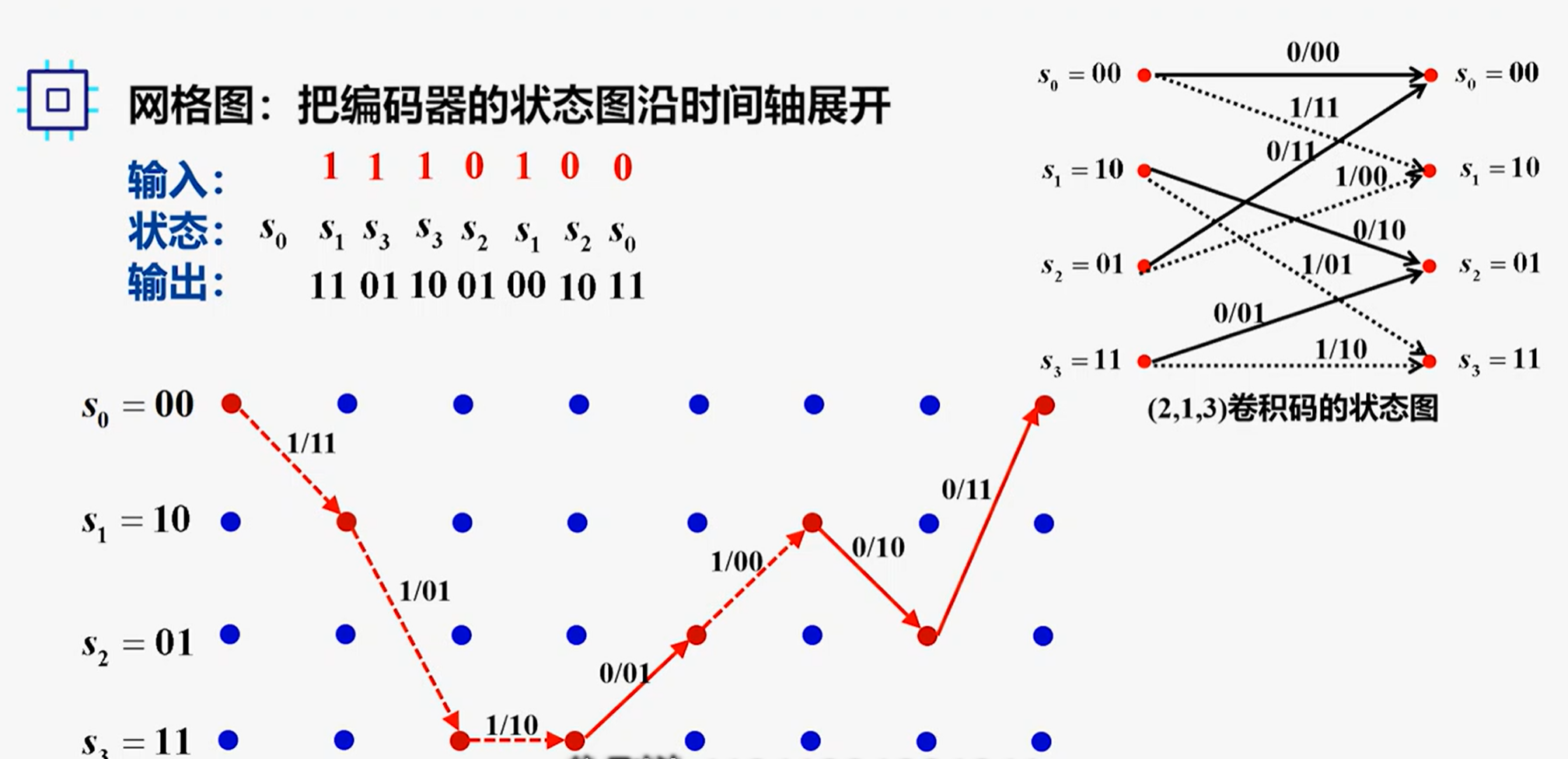
网格图分析——
- 输入中最后2bit是补零操作,是为了让状态寄存器器能恢复成初始状态(X00),不影响下一次序列的输入
卷积码的译码方法—维特比译码
维特比译码是基于动态规划的方法:
- 动态规划思想:当前最优路径=上一步最优路径+当前组合
- 维特比译码思想:译码器每接收一段,就计算比较判决
分支度量:某时刻输出子码与接收子码之间的汉明距离
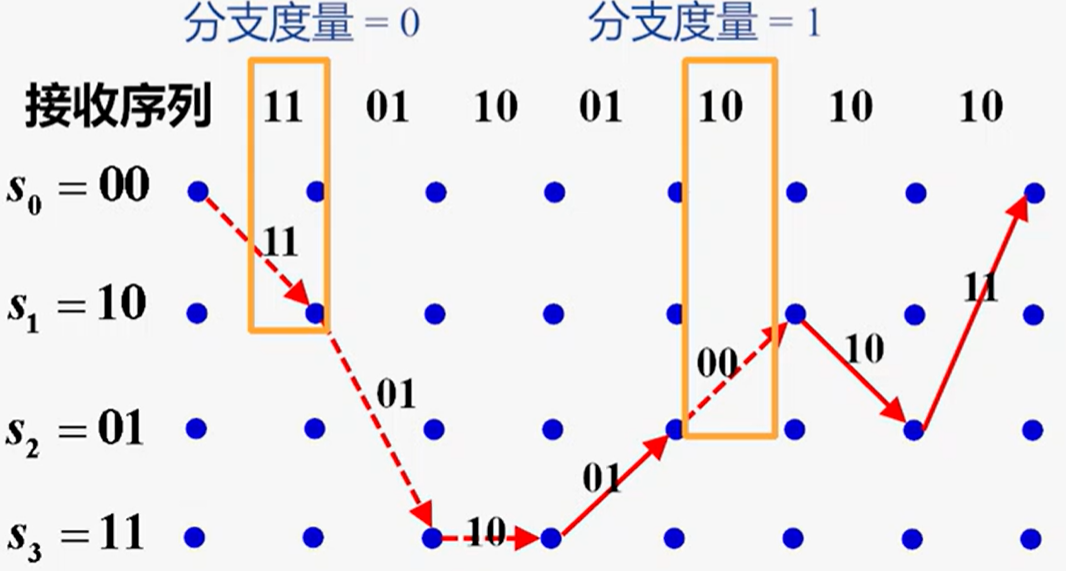
路径度量:
- 该路径输出序列与接收序列之间的汉明距离,是分支度量的和
- 则上述的路径度量=0+0+0+0+1+0+1=2
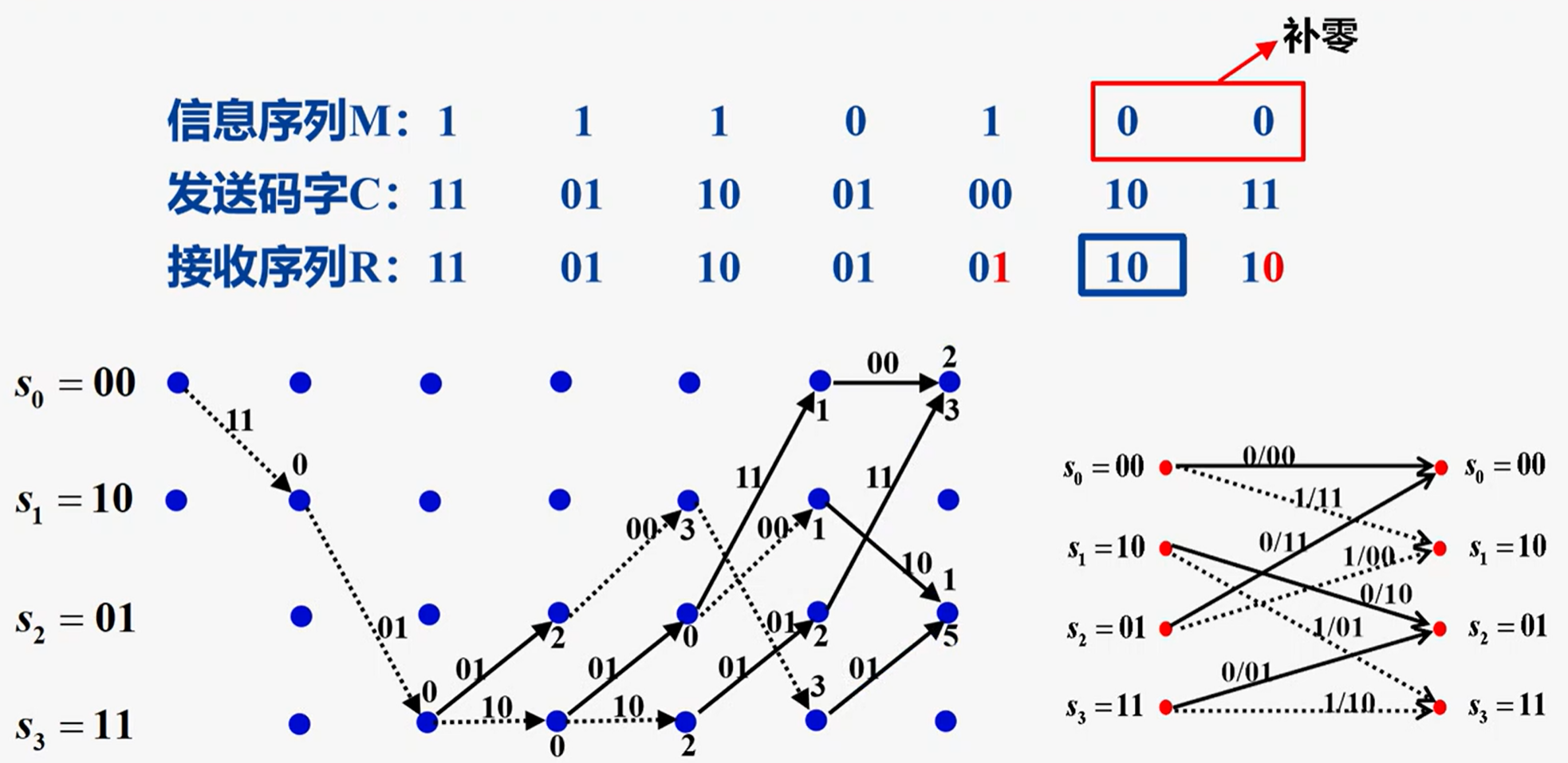
维特比译码步骤:
- 计算到达当前节点的分支度量
- 取出到达上一节点对应的路径度量
- 相加得到两个新路径度量,比较,选择汉明距离较小者,被称为幸存路径
- 具体解释可见:VLSI数字通信原理与设计_中国大学MOOC(慕课) (icourse163.org)
维特比译码的特点:
- 维特比算法是最大似然译码算法
- 运算量和存储量与状态数$2^{km}$呈线性关系
- 运算量和存储量与码长L呈线性关系
截尾译码:
分段译码,降低复杂度
译码深度h,其中m-1为编码器记忆深度
卷积码的性能
自由距离$d_f$的确定:
- 卷积码属于线性码,所以任意两个码序列按位模二加仍然是一个许用码,而它的重量(1的个数)就等于这两个码序列之间的汉明距离
- 只要在所有的码序列中找到最小重量的许用码,它的重量就是卷积码的最小汉明距离
- 任意许用码序列的重量又等于它与全0码之间的汉明距离
- 只要在格图上找到一条离全零距离最近的、从0状态出发又回到0状态的非全0路径,那么这条路径所代表的码序列的重量就等于自由距离
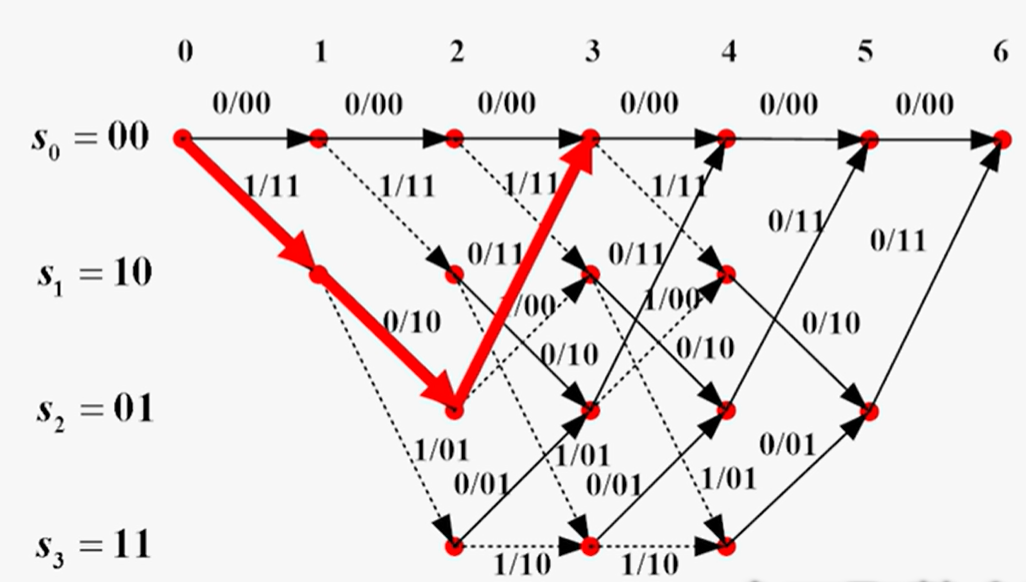
- 则上述中重量最小的路径为:$S_0\xrightarrow{11}S_1\xrightarrow{10}S_2\xrightarrow{11}S_0$
在译码深度长度内,可以纠正$\lfloor\frac{(d_f-1)}{2}\rfloor$个随机错误
卷积码的编码增益:
- 编码增益$dB=[\frac{E_b}{N_0}dB]_{未编码}-[\frac{E_b}{N_0}dB]_{编码}$
- 硬件判决编码增益$dB:10log_{10}(\frac{Rd_f}{2})$
